Which Is a Possible Turning Point for the Continuous Function f(x)? Exploring Possibilities

In mathematics, the concept of turning points is crucial when analyzing functions. A turning point refers to a location on a graph where the function changes direction from increasing to decreasing or vice versa. This article aims to explore the possibilities of a turning point for a continuous function f(x). By understanding the characteristics and properties of turning points, we can gain insights into the behavior of functions. Let's delve into the topic and uncover the potential turning points of a continuous function.

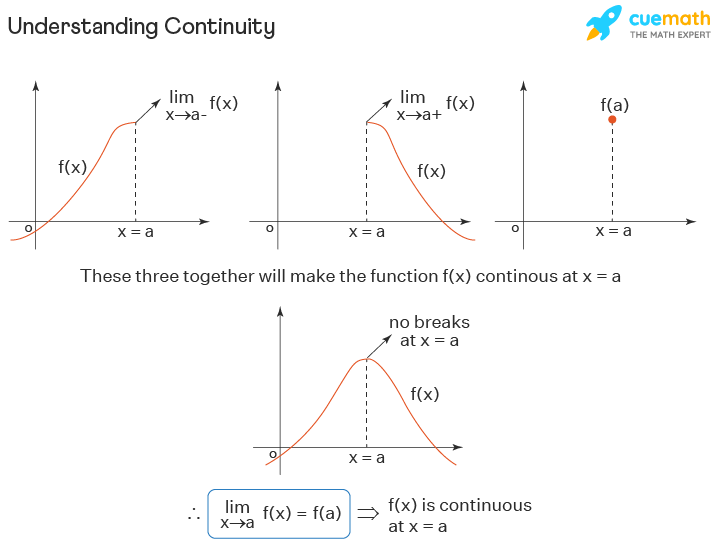
Which is a possible turning point for the continuous function f(x) ?

1. Understanding Continuous Functions

Before discussing turning points, it's essential to grasp the concept of a continuous function.

In mathematics, a function is considered continuous if it is unbroken and has no abrupt jumps or holes in its graph.

A continuous function exhibits a smooth and continuous pattern without any sudden disruptions.

2. Definition of a Turning Point

A turning point, also known as a critical point or extremum, is a specific point on a function's graph where the function changes its direction of change.

It can occur when the function changes from increasing to decreasing (concave down) or from decreasing to increasing (concave up).

At a turning point, the derivative of the function equals zero, indicating a change in slope.

3. Possible Turning Point Scenarios

There are several possible scenarios for the existence of turning points in a continuous function. Let's explore them:

a. Local Minimum/Maximum: A turning point can occur when the function reaches a local minimum or maximum. At these points, the function changes from decreasing to increasing or vice versa. The slope of the function is zero at these points.

b. Inflection Point: An inflection point is another type of turning point where the concavity of the function changes. At an inflection point, the function changes from concave up to concave down or vice versa. However, it's important to note that not all inflection points are turning points, as they can occur without a change in slope.

c. Plateau or Flat Segment: In some cases, a continuous function may exhibit a flat segment where the slope is zero for an extended interval. This segment can be considered a turning point, even though there is no change in the overall direction of the function.

4. Identifying Turning Points

To identify turning points, we need to analyze the behavior of the function's derivative. The derivative provides information about the slope of the function at each point. By setting the derivative equal to zero and solving for x, we can find potential turning points.

5. Example Function

Let's consider the function f(x) = x^3 - 3x^2 + 2x. To find the turning points of this function, we can calculate its derivative, f'(x), which is equal to 3x^2 - 6x + 2. By setting f'(x) = 0 and solving for x, we can find the x-values of potential turning points. In this case, the quadratic equation 3x^2 - 6x + 2 = 0 yields two solutions: x ≈ 0.41 and x ≈ 1.59. These x-values represent the potential turning points of the function.

Student solving math

Turning points play a significant role in understanding the behavior of continuous functions. By analyzing the derivative of a function, we can identify potential turning points where the function changes its direction of change or concavity. Whether it's a local minimum/maximum, an inflection point, or a flat segment, turning points provide insights into the characteristics of functions. By exploring different scenarios and applying mathematical tools, we can unravel the possibilities of turning points in continuous functions.